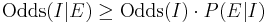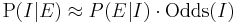Prosecutor's fallacy
The prosecutor's fallacy is a fallacy of statistical reasoning made in law where the context in which the accused has been brought to court is falsely assumed to be irrelevant to judging how confident a jury can be in evidence against them with a statistical measure of doubt. If the defendant was selected from a large group because of the evidence under consideration, then this fact should be included in weighing how incriminating that evidence is. Not doing so is a base rate fallacy. This fallacy usually results in assuming that the prior probability that a piece of evidence would implicate a randomly chosen member of the population is equal to the probability that it would implicate the defendant.
One form of the fallacy results from misunderstanding conditional probability and neglecting the prior odds of a defendant being guilty before that evidence was introduced. When a prosecutor has collected some evidence (for instance a DNA match) and has an expert testify that the probability of finding this evidence if the accused were innocent is tiny, the fallacy occurs if it is concluded that the probability of the accused being innocent must be comparably tiny. The probability of innocence would only be the same small value if the prior odds of guilt were exactly 1:1. If the accused is otherwise totally unconnected to the case, and is only in the courtroom due to that DNA evidence then we should consider a much lower prior probability of guilt, such as the overall rate of offenders in the populace.
The fallacy can arise from multiple testing, such as when evidence is compared against a large database. The size of the database elevates the likelihood of finding a match by pure chance alone; i.e., DNA evidence is soundest when a match is found after a single directed comparison because the existence of matches against a large database where the test sample is of poor quality (common for recovered evidence) is very likely by mere chance.
The terms "prosecutor's fallacy" and "defense attorney's fallacy" were originated by William C. Thompson and Edward Schumann in the 1987 article Interpretation of Statistical Evidence in Criminal Trials, subtitled The Prosecutor's Fallacy and the Defense Attorney's Fallacy.[1][2]
Contents |
Examples of prosecutor's fallacies
Conditional probability
Argument from rarity – Consider this case: a lottery winner is accused of cheating, based on the improbability of winning. At the trial, the prosecutor calculates the (very small) probability of winning the lottery without cheating and argues that this is the chance of innocence. The logical flaw is that the prosecutor has failed to account for the low prior probability of winning in the first place.
Berkson's paradox - mistaking conditional probability for unconditional - led to several wrongful convictions of British mothers, accused of murdering two of their children in infancy, where the primary evidence against them was the statistical improbability of two children dying accidentally in the same household (under "Meadow's law"). Though multiple accidental (SIDS) deaths are rare, so are multiple murders; with only the facts of the deaths as evidence, it is the ratio of these (prior) improbabilities that gives the correct "posterior probability" of murder.[3]
Multiple testing
In another scenario, a crime-scene DNA sample is compared against a database of 20,000 men. A match is found, that man is accused and at his trial, it is testified that the probability that two DNA profiles match by chance is only 1 in 10,000. This does not mean the probability that the suspect is innocent is 1 in 10,000. Since 20,000 men were tested, there were 20,000 opportunities to find a match by chance.
Even if none of the men in the database left the crime-scene DNA, a match by chance to an innocent is more likely than not. The chance of getting at least one match among the records is:
So, this evidence alone is an uncompelling data dredging result. If the culprit was in the database then he and one or more other men would probably be matched; in either case, it would be a fallacy to ignore the number of records searched when weighing the evidence. "Cold hits" like this on DNA databanks are now understood to require careful presentation as trial evidence.
Mathematical analysis
Finding a person innocent or guilty can be viewed in mathematical terms as a form of binary classification. If E is the observed evidence, and I stands for "accused is innocent" then consider the conditional probabilities:
- P(E|I) is the probability that the "damning evidence" would be observed even when the accused is innocent (a "false positive").
- P(I|E) is the probability that the accused is innocent, despite the evidence E.
With forensic evidence, P(E|I) is tiny. The prosecutor wrongly concludes that P(I|E) is comparatively tiny. (The Lucia de Berk prosecution is accused of exactly this error,[4] for example.) In fact, P(E|I) and P(I|E) are quite different; using Bayes' theorem:
Where:
- P(I) is the probability of innocence independent of the test result (i.e. from all other evidence) and
- P(E) is the prior probability that the evidence would be observed (regardless of innocence):
- P(E|~I) is the probability that the evidence would identify a guilty suspect (not give a false negative). This is usually close to 100%, slightly increasing the inference of innocence over a test without false negatives. That inequality is concisely expressed in terms of odds:
The prosecutor is claiming a negligible chance of innocence, given the evidence, implying Odds(I|E) -> P(I|E), or that:
A prosecutor conflating P(I|E) with P(E|I) makes a technical error whenever Odds(I) >> 1. This may be a harmless error if P(I|E) is still negligible, but it is especially misleading otherwise (mistaking low statistical significance for high confidence).
Legal impact
In the courtroom, the prosecutor's fallacy typically happens by mistake,[5] but deliberate use of the prosecutor's fallacy is prosecutorial misconduct and can subject the prosecutor to official reprimand, disbarment or criminal punishment.
In the adversarial system, lawyers are usually free to present statistical evidence as best suits their case; retrials are more commonly the result of the prosecutor's fallacy in expert witness testimony or in the judge's summation.[6]
Defense attorney's fallacy
Suppose there is a one-in-a-million chance of a match given that the accused is innocent. The prosecutor says this means there is only a one-in-a-million chance of innocence. But if everyone in a community of 10 million people is tested, one expects 10 matches even if all are innocent. The defense fallacy would be to reason that "10 matches were expected, so the accused is no more likely to be guilty than any of the other matches, thus the evidence suggests a 90% chance that the accused is innocent." and "As such, this evidence is irrelevant.".
The first part of the reasoning would be correct only in the case where there is no further evidence pointing to the defendant. On the second part, Thompson & Schumann wrote that the evidence should still be highly relevant because it "drastically narrows the group of people who are or could have been suspects, while failing to exclude the defendant" (page 171).[1][7]
A version of this fallacy arose in the O. J. Simpson murder trial: crime scene blood matched Simpson's with characteristics shared by 1 in 400 people. The defense argued that a football stadium could be filled with Angelenos matching the sample, so the evidence was useless.[8] Since there were fewer plausible suspects than the population of Los Angeles, that argument was fallacious.[9]
The Sally Clark case
Sally Clark, a British woman who was accused in 1998 of having killed her first child at 11 weeks of age, then conceived another child and allegedly killed it at 8 weeks of age. The prosecution had expert witness Sir Roy Meadow testify that the probability of two children in the same family dying from SIDS is about 1 in 73 million. That was much less frequent than the actual rate measured in historical data - Meadow estimated it from single-SIDS death data, and the assumption that the probability of such deaths should be uncorrelated between infants. [10]
Meadow acknowledged that 1-in-73 million is not an impossibility, but argued that such accidents would happen "once every hundred years" and that, in a country of 15 million 2-child families, it is vastly more likely that the double-deaths are due to Münchausen syndrome by proxy than to such a rare accident. However, there is good reason to suppose that the likelihood of a death from SIDS in a family is significantly greater if a previous child has already died in these circumstances (a genetic predisposition to SIDS is likely to invalidate that assumed statistical independence[11]) making some families more susceptible to SIDS and the error an outcome of the ecological fallacy.[12] The likelihood of two SIDS deaths in the same family cannot be soundly estimated by squaring the likelihood of a single such death in all otherwise similar families.[13]
1-in-73 million greatly underestimated the chance of two successive accidents, but, even if that assessment were accurate, the court seems to have missed the fact that the 1-in-73 million number meant nothing on its own. As an a priori probability, it should have been weighed against the a priori probabilities of the alternatives. Given that two deaths had occurred, one of two possible explanations must be true, and both of these are a priori extremely improbable:
- Possibility A) Two successive deaths in the same family, both by SIDS.
- Possibility B) Double homicide (the prosecution's case)
It's unclear that an estimate for the second possibility was ever proposed during the trial, or that the comparison of these two probabilities was understood to be the key estimate to make in the statistical analysis of the case.
Mrs. Clark was convicted in 1999, resulting in a press release by the Royal Statistical Society which pointed out the mistakes.[14]
In 2002, Ray Hill (Mathematics professor at Salford) attempted to accurately compare the chances of these two possible explanations; he concluded that successive accidents are between 4.5 and 9 times more likely than are successive murders, so that the a priori odds of Clark's guilt were between 4.5 to 1 and 9 to 1 against.[15]
A higher court later quashed Sally Clark's conviction, on other grounds, on 29 January 2003. However, Sally Clark, a practising solicitor before the conviction, developed a number of serious psychiatric problems including serious alcohol dependency and died in 2007 from alcohol poisoning. [16]
See also
- Base rate fallacy
- Representativeness heuristic
- False positive
- False positive paradox
- Likelihood function
- Howland will forgery trial
- People v. Collins
- Conditional probability fallacy
- Lucia de Berk
- Simpson's paradox
- Data dredging
References
- ^ a b Thompson, E.L.; Shumann, E. L. (1987). "Interpretation of Statistical Evidence in Criminal Trials: The Prosecutor's Fallacy and the Defense Attorney's Fallacy". Law and Human Behavior (Springer) II (3): 167. JSTOR 1393631.
- ^ Fountain, John; Gunby, Philip (February 2010). "Ambiguity, the Certainty Illusion, and Gigerenzer's Natural Frequency Approach to Reasoning with Inverse Probabilities". University of Canterbury. p. 6. http://uctv.canterbury.ac.nz/viewfile.php/4/sharing/55/74/74/NZEPVersionofImpreciseProbabilitiespaperVersi.pdf.
- ^ Goldacre, Ben (2006-10-28). "Prosecuting and defending by numbers". The Guardian. http://www.guardian.co.uk/science/2006/oct/28/uknews1. Retrieved 2010-05-22. "rarity is irrelevant, because double murder is rare too. An entire court process failed to spot the nuance of how the figure should be used. Twice."
- ^ Meester, R.; Collins, M.; Gill, R.; van Lambalgen, M. (2007-05-05). "On the (ab)use of statistics in the legal case against the nurse Lucia de B.". Law, Probability & Risk 5 (3–4): 233–250. arXiv:math/0607340. doi:10.1093/lpr/mgm003. "[page 11] Writing E for the observed event, and H for the hypothesis of chance, Elffers calculated P(E | H) < 0.0342%, while the court seems to have concluded that P(H | E) < 0.0342%"
- ^ Rossmo, D.K. (October 2009). "Failures in Criminal Investigation: Errors of Thinking". The Police Chief LXXVI (10). http://policechiefmagazine.org/magazine/index.cfm?fuseaction=display_arch&article_id=1922&issue_id=102009. Retrieved 2010-05-21. "The prosecutor’s fallacy is more insidious because it typically happens by mistake."
- ^ "DNA Identification in the Criminal Justice System". Australian Institute of Criminology. 2002-05-01. http://www.denverda.org/DNA_Documents/DNA%20in%20Australia.pdf. Retrieved 2010-05-21.
- ^ N. Scurich (2010). "Interpretative Arguments of Forensic Match Evidence: An Evidentiary Analysis". The Darmouth Law Journal 8 (2): 31–47. SSRN 1539107. "The idea is that each piece of evidence need not conclusively establish a proposition, but that all the evidence can be used as a mosaic to establish the proposition"
- ^ Robertson, B., & Vignaux, G. A. (1995). Interpreting evidence: Evaluating forensic evidence in the courtroom. Chichester: John Wiley and Sons.
- ^ Rossmo, D. Kim (2009). Criminal Investigative Failures. CRC Press Taylor & Francis Group.
- ^ The population-wide probability of a SIDS fatality was about 1 in 1,303; Meadow generated his 1-in-73 million estimate from the lesser probability of SIDS death in the Clark household, which had lower risk factors (e.g. non-smoking). In this sub-population he estimated the probability of a single death at 1 in 8,500. See: Joyce, H. (September 2002). "Beyond reasonable doubt" (pdf). plus.maths.org. http://plus.maths.org/issue21/features/clark/. Retrieved 2010-06-12.. Professor Ray Hill questioned even this first step (1/8,500 vs 1/1,300) in two ways: firstly, on the grounds that it was biased, excluding those factors that increased risk (especially that both children were boys) and (more importantly) because reductions in SIDS risk factors will proportionately reduce murder risk factors, so that the relative frequencies of Münchausen syndrome by proxy and SIDS will remain in the same ratio as in the general population: Hill, Ray (2002). "Cot Death or Murder? - Weighing the Probabilities". http://www.mrbartonmaths.com/resources/a%20level/s1/Beyond%20reasonable%20doubt.doc. "it is patently unfair to use the characteristics which basically make her a good, clean-living, mother as factors which count against her. Yes, we can agree that such factors make a natural death less likely – but those same characteristics also make murder less likely."
- ^ Gene find casts doubt on double 'cot death' murders. The Observer; July 15, 2001
- ^ Vincent Scheurer. "Convicted on Statistics?". http://understandinguncertainty.org/node/545#notes. Retrieved 2010-05-21.
- ^ Hill, R. (2004). "Multiple sudden infant deaths – coincidence or beyond coincidence?". Paediatric and Perinatal Epidemiology 18: 321. http://www.cse.salford.ac.uk/staff/RHill/ppe_5601.pdf.
- ^ "Royal Statistical Society concerned by issues raised in Sally Clark case". 23 October 2001. http://www.rss.org.uk/PDF/RSS%20Statement%20regarding%20statistical%20issues%20in%20the%20Sally%20Clark%20case,%20October%2023rd%202001.pdf. "Society does not tolerate doctors making serious clinical errors because it is widely understood that such errors could mean the difference between life and death. The case of R v. Sally Clark is one example of a medical expert witness making a serious statistical error, one which may have had a profound effect on the outcome of the case"
- ^ The uncertainty in this range is mainly driven by uncertainty in the likelihood of killing a second child, having killed a first, see: Hill, R. (2004). "Multiple sudden infant deaths – coincidence or beyond coincidence?". Paediatric and Perinatal Epidemiology 18: 322–323. http://www.cse.salford.ac.uk/staff/RHill/ppe_5601.pdf.
- ^ Shaikh, Thair (March 17, 2007). "Sally Clark, mother wrongly convicted of killing her sons, found dead at home". London: The Guardian. http://www.guardian.co.uk/society/2007/mar/17/childrensservices.uknews. Retrieved 2008-09-25.
External links
- Discussion of the prosecutor's fallacy
- Forensic mathematics of DNA matching
- Thompson, W. C.; Schumann, E. L. (1987). "Interpretation of Statistical Evidence in Criminal Trials: The Prosecutor's Fallacy and the Defense Attorney's Fallacy". Law and Human Behavior 11 (3): 167–187. JSTOR 1393631.
- A British statistician on the fallacy
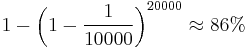
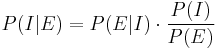
![P(E) = P(E|I) \cdot P(I) %2B P(E|\sim I) \cdot [1 - P(I)]](/2012-wikipedia_en_all_nopic_01_2012/I/2d26b84ae7180e7c260c352b077ff92e.png)